Schema della sezione
-
Gli studenti del primo anno, del corso in Informatica, sono suddivisi in due classi A e B.
In particolare per l'insegnamento di Analisi Matematica, con docenti rispettivamente Carlo R. Grisanti ed Elisabetta Chiodaroli.
Per uniformare vieppiu' l'esposizione degli argomenti e l'allenamento ad affrontare temi di esame comuni, si propone un ciclo di esercitazioni comuni alle due classi, tenute da un terzo docente, Vincenzo M. Tortorelli, ad ognuna della due classi separatamente.
Seguendo l'iter degli argomenti esposti alle due classi, ogni settimana verra' proposta agli studenti delle due classi la stessa selezione di esercizi, scelti dai tre docenti, sottoforma sia di quesiti a risposta aperta, sia a risposta chiusa, senza svolgimento, ed esercizi ove invece sia richiesto uno svolgimento.
L'esposizione dei temi di esercitazione cerchera' di seguire il formato dei testi di esame scritti. In particolare molti dei temi proposti saranno, appunto, scelti dai testi di esame scirtti dei passati anni a cura di Carlo Grisanti.
VMT
ORARI ESERCITAZIONI ``COMUNI''
Di norma:
Sezione A: mercoledi dalle ore 16 alle ore 18 in aula E del polo Fibonacci
Sezione B: venerdi dalle ore 11 alle ore 13 in aula E del polo Fibonacci
RICEVIMENTO
V.M.Tortorelli riceve tutti gli studenti del corso di Analisi Matematica:
- di norma il mercoledi, dopo la lezione alla sezione A, dalle 18,30 in aula E del polo Fibonacci, si prega di preavvisare il docente, almeno il giorno precedente, all'indirizzo
tortorel@dm.unipi.it
- su appuntamento da concordarsi con il docente, per singoli o gruppi.
STRUTTURA DELLA PRESENTE PAGINA
A seguire, in questa colonna centrale compariranno: le istruzioni per ricevere avvisi relativi a queste esercitazioni, il collegamento agli avvisi del docente, un collegamento per consultare delle brevi dispense che riguardano alcuni prerequisiti, il collegamento alle pagine di didattica degli altri due docenti, il collegamento ai rispettivi registri delle lezioni, e, in progressione settimanale, eventuale materiale delle esercitazioni svolte.VMT
-
Con questo collegamento saranno accessibili:
- le note delle lezioni tenute da C.R.Grisanti nell'anno 2015-2016, a cui seguiranno, di volta in volta, quelle dell'attuale anno accademico,
- i temi di esame degli ultimi tre anni con soluzioni,
- il programma dell'insegnamento.
-
-
Domande a risposta chiusa su un ripasso di alcune nozioni e sui primi argomenti svolti a lezione: trigonometria, concetti relativi alle funzioni, grafici e operazioni elementari sui grafici, grafici notevoli, estremo superiore, estremo inferiore, massimo, minimo, limitatezza ...
-
-
-
Definizioni di estremo superiore ed inferiore, complementi sugli allineamenti decimali e relativa primeur sugli infinitesimi
-
-
Dieci domande a risposta chiusa ed un esercizio da svolgere.
-
-
-
Dieci domande a risposta chiusa (simulazione prima parte di esame).
-
-
Ricevimento del 29 Ottobre 2018 in vista della prima prova in itinere.
Prima prova in itinere del 30 Ottobre 2018. -
Esercitazioni: per la sezione A il mercoledi tenute da C.Grisanti, per la sezione B il venerdi da E.Chiodaroli.
-
-
Contiene: un formulario essenziale di trigonometria, di complemento un riassunto sui numeri complessi, e quindi un riassunto sulle equazioni differenziali.
-
A.1)
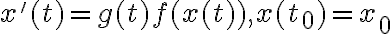 ed
ed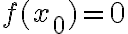 allora
allora 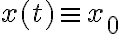 e' soluzione che si dice stazionaria.
e' soluzione che si dice stazionaria.A.2) se
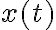 e' soluzione di
e' soluzione di 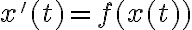 per ogni reale t, allora anche le funzioni
per ogni reale t, allora anche le funzioni 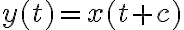 sono soluzioni della stessa equazione.
sono soluzioni della stessa equazione.A.3) Problema dell'unicita' per il problema ai dati iniziali con dato stazionario: non sempre garantita
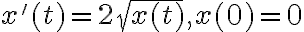 .
.B) Equazioni differenziali del secondo ordine a coefficienti costanti:
impostazione dell'esercizio 2 del fogli della X settimana.
Se M trasforma funzioni in funzioni e M(rf+g) = rM(f) + M(g), f e g funzioni ed r numero [proprieta' di linearita'],allora data una funzione c per trovare tutte le funzioni x che risolvon M(x)=c basta trovare
1) tutte le funzioni z che risolvono M(z)=0,
2) ed un sola funzione y per cui M(y)=c:
le soluzioni saranno tutte e sole le x= y+z.
M (x) = x" +a x' +bx gode della proprieta' di linearita'.